Wavelet Two Channel Filterbank
We had seen the concept of Haar two channel filter bank in the article “Haar Wavelet Filter Bank”
We saw that the analysis filter bank are characterized by decomposition filter while synthesis filter banks are characterized by reconstruction filters.
Instead of coefficients defined by haar wavelet and scaling function.Let us assume that the decomposition filters are $h_{o}[n],h_{1}[n]$ and reconstuction filters are $g_{o}[n],g_{1}[n]$.
Let us look at following generic two channel filter bank
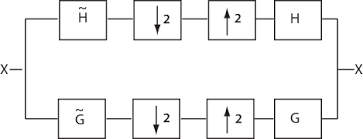
A Perfect Reconstruction filter bank is any filter bank whose reconstruction is the original signal, possibly delayed and scaled version.
Crticially sampled filter banks are ones in which downsampling factor is the same as the number of filter channels.We have filter bank with 2 channels (high pass and low pass decomposition and synthesis) and downsampling factor of 2
We will compute the output at the output of each stage
Analysis Filters
$Y_{1}[z] = H_{o}[z]X[z]$
$Y_{2}[z] = H_{1}[z]X[z]$
Downsampling Block
$X_{down}(z)=\sum_{n=-\infty}^\infty x[Mn] z^{-n} $
Let $m=Mn$, i.e., $n=M/2$, we get $\displaystyle X_{down}(z)$ $\textstyle =$ $\displaystyle \sum_{m=\cdots,-2,0,,2,\cdots} x[m] (z^{1/2})^{m}=\sum_{n} x_{M}[n] z^{-n/M}$
Let $\psi_{M}[n] $ represent a modulation function
$\psi_{M}[n] = \begin{cases}
1, & \text{if}\ mod(n,M) =1 \
0, & \text{otherwise}
\end{cases} $
We can see that $\psi_{M}[n]$ is a periodic impulse function with period of $M$
Thus $\psi_{M}[n] = \frac{1}{M} \sum_{k=0}^{M-1} e^{-j k \omega_{o} n}$
$x_{M}[n]= \frac{1}{M} \sum_{k=0}^{M-1} e^{-j k \omega_{o} n}*x[n]$
$X_{M}(z)= \frac{1}{M} \sum_{n} \sum_{k=0}^{M-1} e^{-j k \omega_{o} n}*x[n] z^{-n}$
$X_{M}(z)= \frac{1}{M} \sum_{k=0}^{M-1} \sum_{n} {e^{-j k \omega_{o} n}*z^{-n} }x[n] $
$X_{M}(z)= \frac{1}{M} \sum_{k=0}^{M-1} \sum_{n} {e^{-j k \frac{2\pi}{M} n}z^{-n} }x[n] $
$X_{M}(z)= \frac{1}{M} \sum_{k=0}^{M-1} X(z * e^{j k \frac{2*\pi}{M}}) $
$X_{down}(z) = \frac{1}{M} \sum_{k=0}^{M-1} X(z^{\frac{1}{M}} * e^{j k \frac{2*\pi}{M}}) $
for M=2 this becomes
$X_{2}(z)= \frac{1}{2} [ X(z^{\frac{1}{2}} ) + X(-z^{\frac{1}{2}} ) ] $
The $X(-z^{\frac{1}{2}} ) $ represents aliasing compnent in downsampling
The output of downsampling block is
$Y_{3}[z]= \frac{1}{2} [ Y_{1}(z^{\frac{1}{2}} ) + Y_{1}(-z^{\frac{1}{2}} ) ] $
$Y_{4}[z]= \frac{1}{2} [ Y_{2}(z^{\frac{1}{2}} ) + Y_{2}(-z^{\frac{1}{2}} ) ] $
Upsampling Block
$X_{o}[z] = X_{in}(z^2)$
$Y_{5}[z]= \frac{1}{2} [ Y_{1}(z ) + Y_{1}(-z)] $
$Y_{6}[z]= \frac{1}{2} [ Y_{2}(z) + Y_{2}(-z) ] $
Synthesis Filtering
$Y_{7}[z]= \frac{1}{2} [ Y_{1}(z ) + Y_{1}(-z)] G_{0}[z]$
$Y_{8}[z]= \frac{1}{2} [ Y_{2}(z) + Y_{2}(-z) ] G_{1}[z]$
Output of FilterBank
$Y(z) = Y_{7}[z]+Y_{8}[z]$
$Y(z) = \frac{1}{2} [H_{0}(z) G_{0}(z) + H_{1}(z) G_{1}(z)] X(z) + [H_{0}(-z) G_{0}(z) + H_{1}(-z) G_{1}(z)] X(-z)$
$Y(z) = \frac{1}{2} [ G_{0}(z) , G_{1}(z) ] \left(\begin{array}{ccc} H_{0}(z) & H_{0}(-z) \ H_{1}(z) & H_{1}(-z)\end{array} \right) \left(\begin{array}{ccc} X(z) \ X(-z) \end{array} \right)$
Thus the output of the filterbank is a linear combination of $X(z) $ and $X(-z)$
The term $X(-z)$ is a consequence of aliasing
$T_{0}(z)$ is component associated with aliasing term.For reconstruction to be possible this should be 0.
In order that output of filter bank recovers $x[z]$ perfectly we require that
$T_{0}(z) = H_{0}(-z) G_{0}(z) + H_{1}(-z) G_{1}(z) = 0$
and $T_{1}(z) = R(z)[H_{0}(z) H_{1}(-z) - H_{1}(z) H_{0}(-z)] =2 $
This gives us a condition that $H_{0}(-z) G_{0}(z) =- H_{1}(-z) G_{1}(z) $
$\frac{G_{0}(z)}{G_{1}(z)} =- \frac{H_{1}(-z)}{H_{0}(-z) } $
A very simple choice is ‘ $G_{0}(z) = R(z) H_{1}(-z)$ $G_{1}(z) = -R(z) H_{0}(-z)$
Two basic constraint for perfect reconstruction filter bank are $T_{1}(z) = R(z)[H_{0}(z) H_{1}(-z) - H_{1}(z) H_{0}(-z)] =2 $ $T_{0}(z) = H_{0}(-z) G_{0}(z) + H_{1}(-z) G_{1}(z) = 0$
As there are four function variables $H_0$, $H_1$, $G_0$ and $G_1$ in the two equations, there exist many possible designs for the filter banks.Some of which are amplitude complimentary filters,quadrature mirror filters,conjugate quadrature mirror filters,orthogonal filters,bi-orthogonal filters etc
Haar filter Bank
$H_{0}[z] = \frac{1}{\sqrt2} [ 1 + z^{-1}]$ $H_{1}[z] = \frac{1}{\sqrt2} [ 1 - z^{-1}]$
$G_{0}[z] = \frac{1}{\sqrt2} [ 1 + z^{-1}]$ $G_{1}[z] = -\frac{1}{\sqrt2} [ 1 - z^{-1}]$
we can see that $T_{0}(z) = H_{0}(-z) G_{0}(z) + H_{1}(-z) G_{1}(z) = 0$
$T_{0}(z) = \frac{1}{2} [ 1 - z^{-1}][ 1 + z^{-1}] - [ 1 + z^{-1}] [ 1 - z^{-1}] =0$
$T_{1}(z) = R(z)[H_{0}(z) H_{1}(-z) - H_{1}(z) H_{0}(-z)] $
$T_{1}(z) = \frac{1}{2} [ 1 + z^{-1}][ 1 + z^{-1}] - [ 1 - z^{-1}][ 1 - z^{-1}]] $
$T_{1}(z) = z^{-1} $
A delay of one sample and $R(z)=2$ for haar wavelets
we can see that Haar wavelets satisfy the criteria for perfect reconstruction
we can also see that if we replace the analysis filters with synthesis filter,the perfect reconstruction criteria is still satisfied