Approximation of Piecewise Polynomial Using Wavelets

Introduction

In this article we look at Approximation of Piecewise Polynomial Using Wavelets

Wavelet Approximation of polynomials

In many application,one needs to approximate a signal using scaling function ie using projection on $V_{m}$ subspace.

The support of a function is the set of points where the function is not zero-valued,The support of $\phi(t),\psi(t)$ which is defined over unit interval is 1

The basic analysis starts with considering a set of monomials ${1,t,t^2,\ldots,t^{k} }$ and asking the question till what degree $k$ can these be reproduced exactly using the scaling function.

Let us assume that $t^{p}$ can be represented exactly using the scaling function $t^{p} = \sum_{k} d_{k} \phi(t - k)$

Orthonormality of basis function impies

$d_{k} = \int t^{p} \phi(t -k ) dt$

To achieve this the scaling function should possess a certain properties which is dependent on the filter coefficients .

Restrictions on scaling and wavelet function

This assumption will impose certain restriction on the scaling and wavelet function

$\int t^{p} \psi(t) dt = \int \sum_{k} d_{k} \phi(t - k)\psi(t) dt = \sum_{k} d_{k} \int \phi(t - k)\psi(t) dt $

$\psi(t) ,\phi(t)$ are orthogonal ,meaning that $\phi(t)$ is capable of expressing polynomials upto degree $p$ exactly.

The projection of $t^{p} $ on $W_{m}$ subspace is 0. The projection of $t^{p} $ on $W_{m}$ subspace will not be zero only when it cannot be expressed completely by the scaling function.

if $p=0$,The condition implies

$\int \psi(t) dt =0$

Indicating that a constant function can always be expressed completely by scaling function.

we know that

$\psi(t) = \sum_{k} g[k] \phi(2t - k)$

$\phi(t) = \sum_{k} h[k] \phi(2t -k )$

We will use a result here which will be derived in later articles

$\int \psi(t) \phi(t) dt =0$ for this to hold true

$g[k]=(-1)^{N-k-1}h(N-k-1)$ and

$\psi(t) = \sum_{k} (-1)^{N-k-1}h(N-k-1) \phi(2t + k -N+1)$

for even N

$g[k]=(-1)^{k}h(N-k-1)$

$\int \sum_{k} (-1)^{N-k-1}h(N-k-1) \phi(2t + k -N+1) dt=0$

$\sum_{k} (-1)^{k} h(k) \int \phi(y) dy=0$

Vanishing Momemnt Constraint on wavelet filter coefficients

Zero order vanishing moment constraint $\sum_{k} (-1)^{k} h(k) =0$

pth order vanishing moment constraint $\sum_{k} (-1)^{k} k^{p}h(k) =0$

These vanishing moment constraint imposed on scaling and wavelet function help solve for the filter coefficients.

Projection of polynomials on subspace defined by Wavelets

Wavelet function $\psi(t)$ having N vanishing moments will kill polynomial upto degree $p-1$

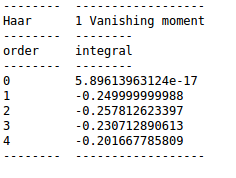
Let us look at a Haar wavelets function and projection of increasing order of polynomials on Haar wavelet basis.Haar wavelet has 1 vanishing moment.

Thus it can only kill polynomial of order 1 or constant function

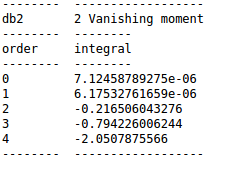
Daubechies -2 wavelet has vanishing moment of 2 ,Thus it can kill polynomial upto degree of 2 A constant and linear function.

Daubechies -4 has vanishing moment of 4 ,Thus it can kill polynomials upto a degree of 3

What this means is that projection on $W_{o}$ subspace is zero.Wavelet coefficients will have low magnitude .Typically threshold should be less than $1^{-7}$.This will imply signal can be reconstructed from the projection on $V_{0}$ subspace to a great degree of accuracy

We can see the projection on the $V_{0}$ and $W_{0}$ subspace in the below figures

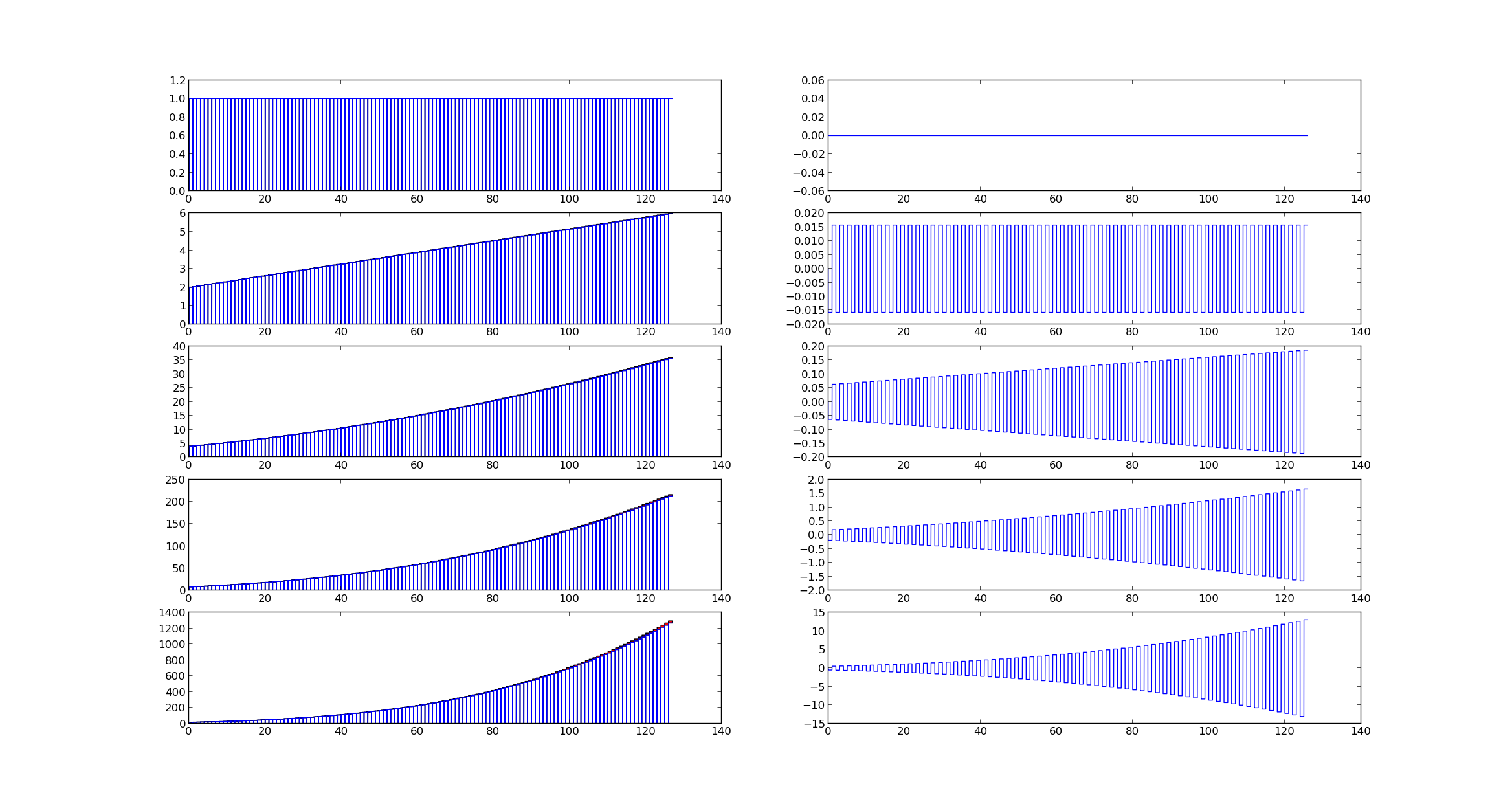
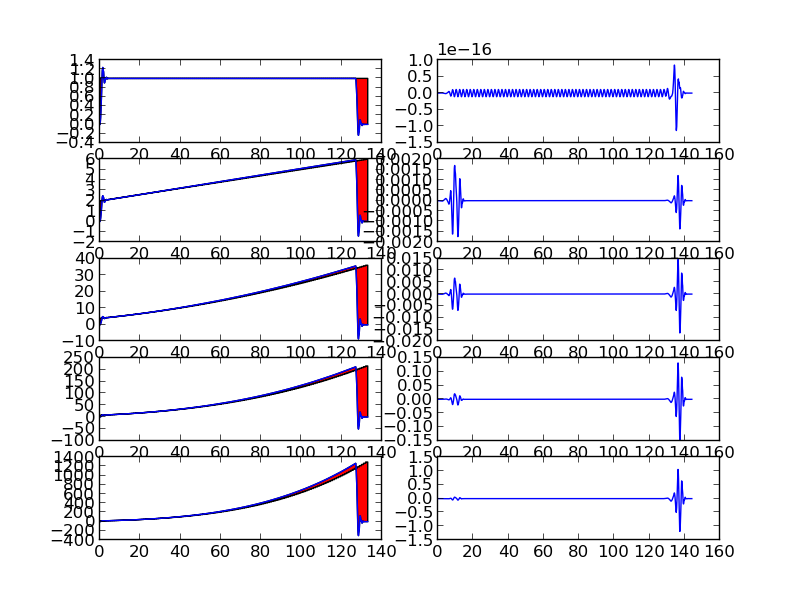
Projection of Piecewise polynomials on subspace defined by Wavelets

It is important to note that it is sufficient that function behaves like a polynomial of degree $k$ over support of function for it to be approximated by scaling function.

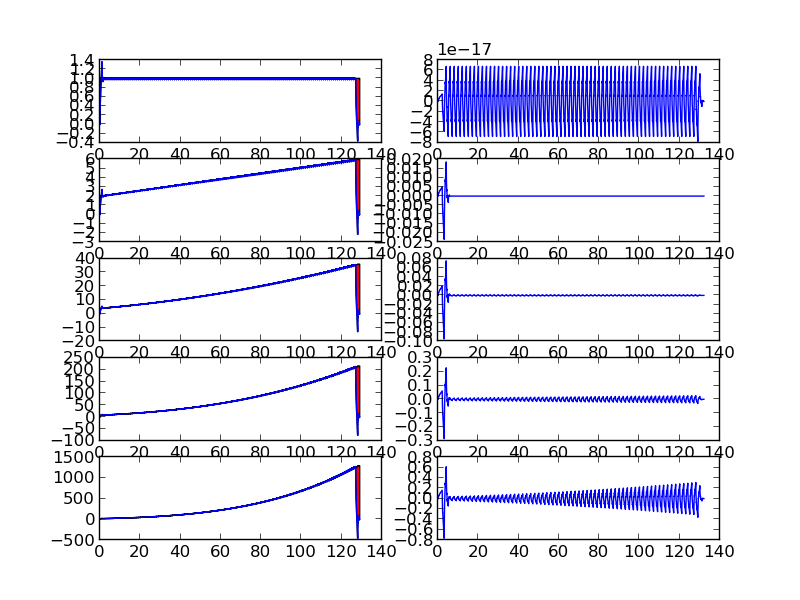
Below figures show piecewise polynomials and projection on $V_{0}$ and $W_{0}$ subspace

We can see that piece-wise polynomials of degree $p$ within the support of wavelet functions with vanishing moment $p$ have zero wavelet coefficients except at points of discontinuity

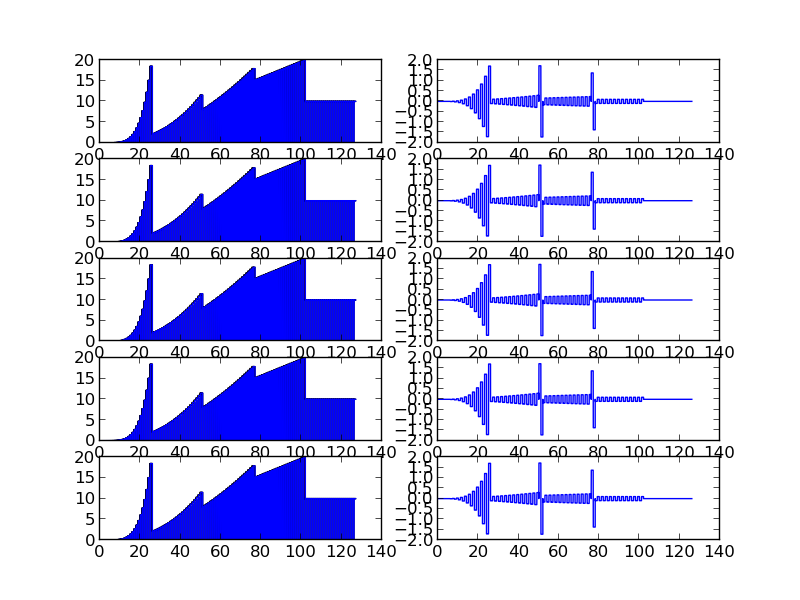
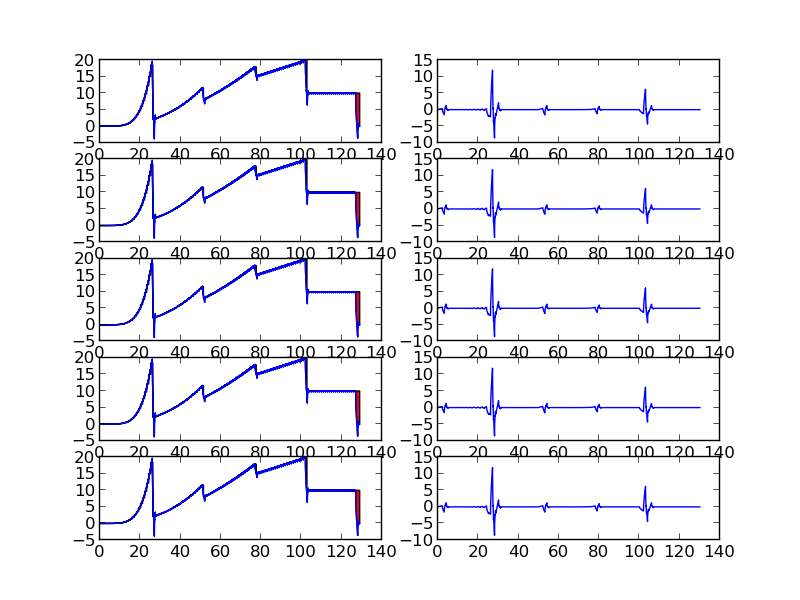
Code

The function plotwaveletProjection plots the projection of signal onto the $V_{m}$ and $W_{m}$ subspace

def plotWaveletProjection(x,coeff,w,level=1,mode=0):
    """ function plots the projection of signal on the scaling and wavelet functions subspace
    
    Parameters
    -----------
    x           : numpy-array,
                  The input signal
             
    coeff      : numpy=-array
                 The wavelet or scaling coefficient
                 
    w           : pywt.Wavelet
                  wavelet object
                  
    level       : integer
                  decomposition level
                  
    mode        : integer
                  scaling or wavelet coefficient
             
        
    Returns
    --------
    out : numpy-tuple
          (time,reconstruction,signal)
    
    """
    
    #generate the scaling and wavelet functions
    s1,w1,t2=w.wavefun(level=20)
    #setup 1D interpolating function for scaling and wavelet functions
    wavelet=interpolate.interp1d(t2, w1)
    scaling=interpolate.interp1d(t2, s1)
    
    
    time=[]
    sig=[]
    s1=np.array(s1,float)
    
   
    #compute the dydactic scale
    l=2**level
    
    #find the support
    end1=math.floor(t2[len(t2)-1])
    d=abs(float(len(coeff))*float(l)-len(x))
    d=int(d)
    
    #range over each element of coefficient
    for i in range(len(coeff)-1):
       
       #define the interpolation points
       t=np.linspace(l*i,l*i+l*end1,l*end1*(len(x)));
       
       t1=np.linspace(0,end1,end1*(len(x))*l);
       
       #multiply the coefficient value with scaling or interpolation function
       if mode==0:
           val=coeff[i]*scaling(t1)
       else:
           val=coeff[i]*wavelet(t1)
           

       ratio=end1
       #compute the translation
       inc=len(t)/ratio
       
       
       if i==0:
               sig=np.append(sig,val)
               time=np.append(time,t)
               
       else:
               #compute the incremental sum of signals
               v1=val[0:len(t)-inc]
               
               if  inc &lt len(t):
                   v2=val[len(t)-inc:len(t)]
                   sig[i*inc:i*inc+len(t)]=sig[i*inc:i*inc+len(t)]+v1
                   sig=np.append(sig,v2)
                   time=np.append(time,np.linspace(l*i+l*end1-l,l*i+l*end1,inc))       
               else:
                   sig=np.append(sig,val)
                   time=np.append(time,t)      
    
    #flatten the arrays
    sig=np.array(sig).flatten()
    time=np.array(time).flatten().ravel()

    #scale the values due to didactic decomposition
    sig=sig/(math.sqrt(2)**level)

    #upsamples the value of signal
    x=np.repeat(x,len(sig)/len(x))

    #return the signals,which can be plotted
    return time,sig,x
    
 

A class called “PiecewiseContinuous “ encapsulates all the methods that define a piece-wise continuous function.The function is modified version of the function from sagemath library

 # piecewise function
def f1(x):return 10
def f2(x):return 5*x
def f3(x):return 2*(x)**2
def f4(x):return (x)**3+(x)**2
def f5(x):return 20*((x)**5)

f = Piecewise([[(0,1),f5],[(1,2),f4],[(2,3),f3],[(3,4),f2],[(4,5),f1]])

f(1) will give the value the value of piecewise function at 1

All the plots and results presented in the article can be generated by running the wavelet4.py files

Files

The code can be found in pyVision github repository

• pyVision/pySignalProc/tutorials/wavelet4.py
• pyVision/pySignalProc/wavelet/pywtUtils.py